Decisioni tree를 이해하기 위해서는 먼저 몇 가지 이해해야 하는 것들이 있습니다.
엔트로피 (entropy) 개념부터 설명하겠습니다.
상상을 해 봅시다.
주머니가 1개 있고, 그 안에 두 가지 종류의 구슬들이 섞여 있다고 합시다.
구슬의 색깔을 빨간색과 흰색으로 상상해 봅시다.
빨간 색과 흰 색의 구슬이 반반씩 섞여있는 경우, 주머니 안을 들여다보면 알록달록해 보일겁니다.
이번에는 빨간 색만 있는 경우를 상상해 보면, 전혀 알록달록 하지 않을 겁니다.
흰 색만 있는 경우도 아주 차분하게, 알록달록 하지 않을 겁니다.
이제 이런 현상에 조금 전문적인 용어를 붙여 봅시다.
알록달록한 정도를 엔트로피 (entropy)라고 합시다.
그러면, 구슬이 반반씩 섞인 경우는 엔트로피가 높다고 할 수 있고,
한 가지 구슬만 있는 경우는 엔트로피가 낮다고 할 수 있다.
즉, 구슬 색깔이 균일할 수록 엔트로피가 낮은 것입니다.
여기서 소개한 용어, Entropy에 대해 직관적으로 이해했기를 바랍니다.
다음에는 엔트로피를 숫자로 표현하는 방법에 대해 다룹니다.
알록달록한 정도, 즉 엔트로피를 숫자로 표현해 보고자 합니다.
엔트로피가 높을 수록 커지는 숫자, 반대는 작아지는 숫자를 만드는 방법이 필요합니다.
이것을 위해서 아래 함수가 필요합니다.
아래 수식과 그래프를 봅시다.


x의 값을 0에서 1.0까지만 고려해 보고, 그 때의 y값을 봅시다.
x가 0에 가까운 값을 가지거나, 1.0에 가까울 때 y값이 작습니다.
x가 0.3 ~ 0.5일때 y값이 큽니다.
이 함수의 특징을 잘 이해해 했으면, 다음으로 넘어갑시다.
이제 구슬과 위 함수를 연결해 봅시다.
x를 주머니 구슬의 비율이라고 합시다.
주머니에는 빨간 색과 흰 색 구슬이 반반 섞여 있으므로, 빨간 색의 비율은 0.5, 흰 색 구슬 비율도 0.5입니다.
이 때, 주머니의 빨간 구슬에 의한 엔트로피를 아래와 같이 표시한다고 합시다.

그런데, 주머니에는 흰 구슬도 있으므로 주머니의 전체 엔트로피는 아래와 같이 표현됩니다.

주머니에 빨간 구슬만 있는 경우,
x = 1.0이 되므로, 흰색은 고려할 필요없이, 엔트로피, 즉 알록달록한 정도는 아래와 같이 0.0이 됩니다.


을 이용하면 주머니 안 구슬배합의 알록달록한 정도를 나타낼 수 있다는 것 감이 잡힐 것입니다. 왜냐하면, 반반씩 섞였을 때 엔트로피는 0.3, 한 가지 구슬만 있을 때는 0.0입니다. 따라서 알록달록할 수록 엔트로피가 커진 것입니다. 다른 비율의 조합들을 시도해 보면 좀 더 이해가 잘 될 겁니다.
주머니와 구슬 비유 안에서 엔트로피를 수학적으로 정의하겠습니다.
주머니 안에 들어있는 색깔별 구슬의 비율을 x_i라고 하면,
그 주머니의 엔트로피는 다음과 같습니다.

예를 들어, x_1은 빨간구슬의 비율, x_2는 흰 구슬의 비율 이렇게 말입니다.
이렇게 정의된 엔트로피는 주머니 안의 구슬 색깔들이 균일할 수록 값이 작습니다.
알록달록할 수록 값이 큽니다.
그래서 엔트로피의 정의는 "무질서도"입니다.
주머니 안에 여러 색깔의 구슬들이 섞여있을수록 무질서하다고 보면 됩니다.
엔트로피 개념에 대해서 직관적으로 이해했으니, decison tree로 다시 돌아가겠습니다.
Decison tree 설명을 위해서 주머니와 구슬 비유를 계속해서 사용하겠습니다.
구슬들이 섞여있는 상황에서 주머니 안에 작은주머니들을 만들고, 구슬들을 나눠서 다시 넣는 상상을 합시다.
아래 그림처럼 말입니다.
작은주머니가 2개 생겼고, 거기에 구슬들을 나눠 담았습니다.
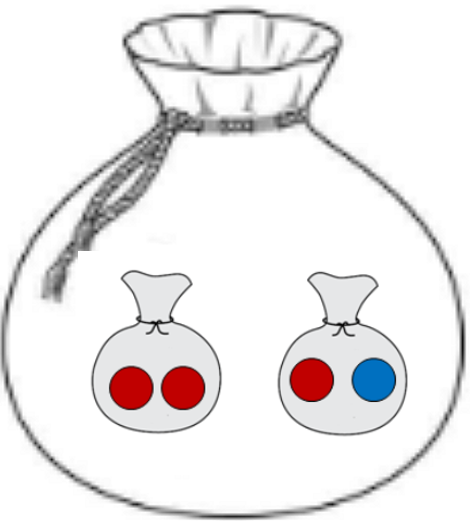
이 때, 작은주머니들의 엔트로피를 구할 수 있을 것입니다.
왼쪽 작은주머니의 엔트로피는 0일 것이고, 오른쪽은 0.3 정도 될 것입니다.
엔트로피가 0이된 왼쪽 주머니는 그대로 두고,
오른쪽 작은주머니 안에 "작은작은주머니들"을 만들어서 구슬을 또 나눠 담을 수 있을 겁니다.
이러한 과정을 엔트로피가 0이 될 때까지 계속해서 반복하다 보면,
새로 만들어진 작은주머니들에는 같은 색깔의 구슬들만 담겨있을 겁니다.
즉, 엔트로피가 0이 된 것입니다
Decision tree의 동작 과정 중 중요한 것은
엔트로피 0를 만드는 것입니다.
즉, 구슬들을 작은주머니들에 나눠담아 가면서, 작은주머니들이 한 가지 색깔의 구슬만 담을 수 있도록 하는 것입니다.
Decision tree의 목적을 알면 왜 이런 과정이 필요한지 이해가 됩니다.
Decision tree는 일반적으로 분류를 하기 위한 방법입니다.
예를 들어서, 메일이 도착했는데 스팸 메일인지 아닌지를 구분한다든지,
제품이 불량인지 양품인지,
꽃의 특성을 보고 어떤 꽃인지 분류하는 일을 하는 것입니다.
여기서 엔트로피 개념이 필요한 이유는,
Decison tree는 분류 결과의 entropy = 0을 만들어 가는 분류 체계를 말합니다.
즉, 같은 것끼리 모아가는 과정을 말합니다.
엔트로피 개념과 decision tree의 기본 동작원리를 설명을 마쳤습니다.
이제는 decision tree를 아주 구체적인 예를 들어서 설명하겠습니다.
메일이 도착했을 때, 스팸 (spam) 메일인지, 아닌지를 구분하는 decision tree를 만들어보겠습니다.
참고로, 스팸메일이 아닌 정상 메일은 햄 (ham )메일이라고 합니다.
Decision tree를 만들기 위해서는 스팸과 햄 메일 관련한 학습데이터가 필요합니다.
학습데이터는 각 메일의 특징을 정리해 두어야 합니다.
여기서는 각 메일의 특징을 3개로 추렸다고 가정하겠습니다.
- 길이 : long, short, 메일의 길이를 나타내는 두 가지 타입
- 이미지포함여부 : yes, no 두 가지 타입으로 메일 내에 이미지가 들어 있는지
- 비트코인 단어 포함여부: yes, no 두가지 타입
아래와 같은 학습데이터를 모았다고 가정하겠습니다.
| 분류 | 속성: 길이 |
속성: 이미지 포함여부 |
속성: 비트코인 단어 포함여부 |
| Spam | long | Y | Y |
| Spam | long | N | Y |
| Spam | long | N | Y |
| Spam | short | N | N |
| Spam | long | Y | Y |
| Ham | long | Y | N |
| Ham | long | Y | N |
| Ham | long | Y | N |
| Ham | short | Y | N |
| Ham | short | Y | Y |
이러한 학습데이터가 주어졌을 때, decision tree는 속성을 기준으로 메일을 나눕니다.
예를 들어, 길이 속성을 기준으로 나눈다면 long과 short 기준에 따라서 메일들을 나눌 것이고,
이미지 포함 여부 속성이라면 Y 또는 N일 것입니다.
어떤 속성을 가지고 나눌지가 핵심인데,
가장 좋은 속성은 Spam과 Ham을 정확하게 구분해 주는 속성이 최고일 것입니다.
그 속성을 찾아내는 방법은,
사용할 수 있는 속성 1) 길이, 2) 이미지, 3) 비트코인에 대해서
각 속성의 값을 기준으로 학습데이터를 나눠보고, 그 분류 안에서 Spam과 Ham이 어느 정도 분리가 되었는지를 평가해서, 가장 분류가 잘 된 것을 기준으로 나누면 될 것입니다.
분류가 잘 되었다는 것은, "덜 알록달록", 즉, "Spam과 Ham"이 덜 섞인 것이므로 엔트로피와 관련이 높습니다.
그렇다면, 정리가 됩니다.
길이 속성값인 long과 short를 기준으로 분류하고, 그 분류된 것에 대해서 엔트로피 값을 구합니다.
마찬가지로 이미지와 비트코인 속성을 기준으로도 엔트로피 값을 구합니다.
그렇게 구해진 엔트로피 값 중에서 최소값을 가지는 속성을 기준으로 일단 메일을 분류하면 되겠습니다.
길이 속성값 long과 short를 기준으로 메일을 분류해 보면 그 결과는 다음과 같습니다.
| 속성 길이 | Spam 비율 | Ham 비율 | 엔트로피 |
| long | 4/7 | 3/7 | 0.2965 |
| short | 1/3 | 2/3 | 0.2764 |
따라서 길이 속성에 따른 엔트로피는 0.2965 + 0.2764가 됩니다.
꽤 높기 때문에 길이는 Spam과 Ham 구분에 별로 도움이 안되는 것을 알 수 있습니다.
이미지 속성값 Y과 N을 기준으로 메일을 분류해 보면 그 결과는 다음과 같습니다.
| 속성 이미지 | Spam 비율 | Ham 비율 | 엔트로피 |
| Y | 2/7 | 5/7 | 0.2598 |
| N | 3/3 | 0/3 | 0 |
이미지 속성에 따른 엔트로피는 0.2598이 됩니다.
비트코인 속성값 Y과 N을 기준으로 메일을 분류해 보면 그 결과는 다음과 같습니다.
| 속성 이미지 | Spam 비율 | Ham 비율 | 엔트로피 |
| Y | 4/5 | 1/5 | 0.217 |
| N | 1/5 | 4/5 | 0.217 |
비트코인에 따른 엔트로피는 0.217 + 0.217입니다.
따라서 이미지 속성에 따른 엔트로피가 가장 낮기 때문에
이미지 속성으로 일단 구분하면 좋을 것 같습니다.
직관적으로 보아도, 이미지가 없는 메일들은 일단 spam 메일로 분류가 됩니다. (물론 현실상황은 그렇지 않지만, 예제를 위해서 그냥 넘어가도록 하겠습니다.)
이렇게 해서 1차적으로 구성된 decision tree는 아래와 같은 모양이 됩니다.
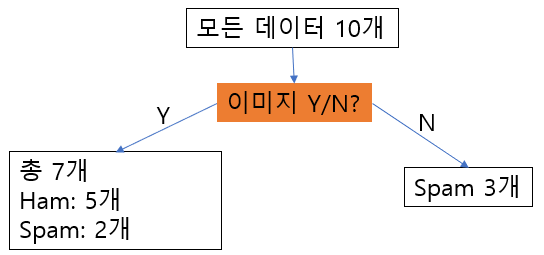
이미지=No인 경우는 모두 spam으로 분류되고,
이미지=Yes인 경우는 ham과 spam이 각각 5개, 2개로 섞여 있게 됩니다.
그러면 다음 단계는, 위 그림에서 왼편 7개 메일에 대해서 entropy를 가장 작게 하는 분류 기준을 찾아내면 됩니다.
물론, 이미지 유무 기준은 더이상 사용할 수 없을 겁니다.
아래 표는 7개 이미지에 대한 데이터만 따로 뽑아 놓은 것입니다.
| 분류 | 속성: 길이 |
속성: 이미지 포함여부 |
속성: 비트코인 단어 포함여부 |
| Spam | long | Y | Y |
| Spam | long | Y | Y |
| Ham | long | Y | N |
| Ham | long | Y | N |
| Ham | long | Y | N |
| Ham | short | Y | N |
| Ham | short | Y | Y |
위의 데이터에 대해서, '길이' 속성과 '비트코인 유무' 속성에 대해서 각각 엔트로피를 계산해 보겠습니다.
첫 번째로, 길이 속성에 대한 entropy는
Long에 대해서는 ham 3개, spam 2개이므로
entropy_long = -(3/5)log(3/5) - (2/5)log(2/5) = 0.29
Short에 대해서는 ham 2개 이므로
entropy_short = 0입니다.
따라서 Entropy_길이 (길이 속성에 대한 entropy) = 0.29입니다.
두 번째로, 비트코인 유무에 대한 entropy는
Yes에 대해서는 ham 1개, spam 2개 이므로
entropy_yes = -(1/3)log(1/3)-(2/3)log(2/4) = 0.27
No에 대해서는 ham 4개이므로,
entorpy_no = 0입니다.
따라서 Entropy_비트코인 (비트코인 단어 유무에 대한 entropy) = 0.27
결론을 내리자면, 비트코인 유무를 판단기준으로 하는 것이 entropy를 낮추는데 도움이 되므로, decision tree의 2번째 단계는 이것을 사용하겠습니다. 이렇게 만들어진 decision tree는 아래와 같습니다.

이제 위 그림의 왼쪽 3개에
ham과 spam이 섞여 있는 것만 풀면 됩니다.
남아있는 데이터는 아래와 같습니다.
| 분류 | 속성: 길이 |
속성: 이미지 포함여부 |
속성: 비트코인 단어 포함여부 |
| Spam | long | Y | Y |
| Spam | long | Y | Y |
| Ham | short | Y | Y |
이제 남아 있는 속성은 길이 밖에 없으므로,
적용해 보면
길이=long의 경우, spam만 2개 이므로 entropy = 0
길이=short의 경우, ham만 1개 이므로 entropy = 0
완벽한 분리가 됩니다.
최종적으로 만들어진 decision tree는 아래와 같습니다.
새로운 test data가 주어지면,
이러한 decision tree를 위에서부터 아래로 단계적으로 거쳐 가면서 분류하면 됩니다.
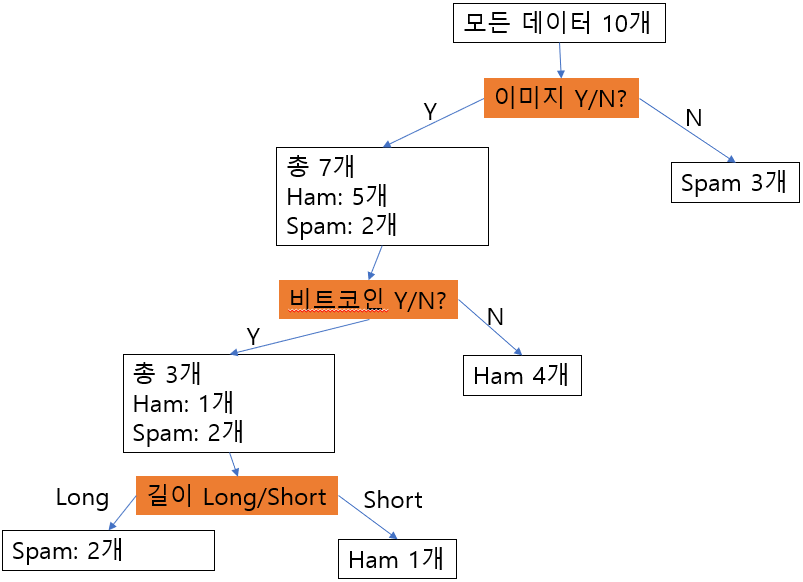
여기서 다룬 decision tree는 매우 간단한 예제에 대한 것인데,
핵심 개념들은 모두 포함하고 있으니,
더 복잡한 경우는 이의 응용으로 보면 되겠습니다.
'머신러닝' 카테고리의 다른 글
| 파이토치 모델 저장; pytorch model save (0) | 2022.11.06 |
|---|---|
| 파이토치(Pytorch) Distributed Data Parallel (DDP)사용하기 (0) | 2022.10.30 |
| 파이토치 모델 로딩, pytorch model loading (0) | 2022.10.27 |
| Pytorch Simple - 1. Autograd (0) | 2019.09.09 |
| 사진에 나온 얼굴에서 감정을 읽는 Emotion API (0) | 2018.07.22 |


